MS 095 PreAlgebra Volume and Significant Digits Laboratory

Volume theory

The volume of a box is Length × width × height or Lwh.

The volume of a cylinder is π r²L

The volume of a sphere is (4π r³)/3

Obtain a ruler and a box, cylinder, or a sphere. Some groups will start with a box, some with a cylinder, and others with a sphere. During the laboratory each group will measure a box, cylinder, and a sphere.

Experimental Procedure

1. Box

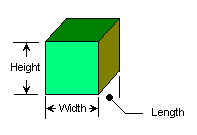
   1. Measure the Length, width, and height of the box to an accuracy of one millimeter.
      
      Length L: ________ Width w: ________ Height h: ________
   2. Calculate the volume of the box by multiplying the Length × Width × Height.
      
      Volume ___________________  (be sure to include the correct units!)
   3. Record your Volume on the white board in the box column at the front of the room.
   4. When every group has recorded their box volume, note the largest and the smallest volume shown on the board.
      
      Largest volume ________________ Smallest volume ________________
   5. Calculate the average volume of the box by adding all of the volumes on the board and then dividing by the number of measurements  of volume made:
      
      Average  =  Sum of the volumes/Number of measurements = _______________
   6. Make the following calculations:
      
      Upper half range = Largest volume - Average volume = _____________
      
      Lower Half range = Average volume - Smallest volume ______________
      
   7. Fill in the blanks to record the experimentally determined Volume of the box:
      
      ____________    ____________    ______________
      Average volume + Upper half range - Lower Half Range

2. Cylinder

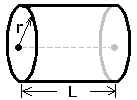
   1. Measure the radius, and Length of the cylinderox to an accuracy of one millimeter.
      
      radius r: ______________ Length L: _____________
   2. Calculate the volume of the cylinder by multiplying the πr²L.
      
      Volume ___________________  (be sure to include the correct units!)
   3. Record your Volume on the white board in the cylinder column at the front of the room.
   4. When every group has recorded their cylinder volume, note the largest and the smallest volume shown on the board.
      
      Largest volume ________________ Smallest volume ________________
   5. Calculate the average cylinder volume by adding all of the volumes on the board and then dividing by the number of measurements  of volume made:
      
      Average cylinder volume  =  Sum of the volumes/Number of measurements = _______________
   6. Make the following calculations:
      
      Upper half range = Largest volume - Average volume = _____________
      
      Lower Half range = Average volume - Smallest volume ______________
      
   7. Fill in the blanks to record the experimentally determined Volume of the cylinder:
      
      ____________    ____________    ______________
      Average volume + Upper half range - Lower Half Range

3. Sphere

   1. Measure the radius of the sphere to an accuracy of one millimeter.
      
      radius r = _________________
   2. Calculate the volume of the sphere using the formula for the volume of a sphere:
      
      Volume sphere = ( 4 π r³)/3
      
      Volume ___________________  (be sure to include the correct units!)
   3. Record the Volume on the white board in the sphere column at the front of the room.
   4. When every group has recorded their sphere volume, note the largest and the smallest volume shown on the board.
      
      Largest volume _____________ Smallest volume ______________
   5. Calculate the average sphere volume by adding all of the volumes on the board and then dividing by the number of measurements  of volume made:
      
      Average sphere volume =  Sum of the volumes/Number of volume measurements = _______________
      
   6. Make the following calculations:
      
      Upper half range = Largest volume - Average volume = _____________
      
      Lower Half range = Average volume - Smallest volume ______________
   7. Fill in the blanks to record the experimentally determined Volume of the sphere:
      
      ____________    ____________    ______________
      Average volume + Upper half range - Lower Half Range

Theory

Suppose a cube has a Length L with an uncertainty e in that length measurement.   The Length of one side is therefore L ± e.  The volume is equal to (L ± e)³.  [Expand this binomial as a group exercise.]

The expansion is L³ ± L²e + L e² ± e³.  L³ is the true volume of the cube. Note that the third term, L e² is always positive (e² is positive even for a negative error) and therefore always tends to increase the volume.  The term that causes the most "problems" in terms of accuracy is L²e.  L²e is an uncertainty in the area due to uncertainty in the length of the edges of the area.  This term can be quite large due to the L².  If a cube is five centimeters on an edge and the uncertainty is one millimeter, then this term is plus or minus 2.5 cm³.  Similar arguments can be made for any volume calculation, there is always an areal error that is "large" compared to the error in measurement of the length of a edge.

These same arguments apply to the calculations of the volume of the sphere.

Application: Significant Digits

When adding numbers simply add the numbers and keep the result.  This is not wholly correct, but without being able to calculate an actual experimental error in each measurement this procedure will have to suffice.

When multiplying numbers, count the number of digits in each measurements.  Keep the number of significant digits that is equal to the number of the digits in the measurement with the fewest digits.

5.4 cm + 11.9 cm  + 101.5 cm = 118.8 cm

Often, when adding, the number of decimal places in the measurements will be the same.   In this case the number of decimal places in the answer agrees with the number of decimal places in the answer.

5.4 cm × 11.9 cm  × 101.5 cm = 6522.39 cm³ = 6500 cm³

Note that only the 6 and the 5 were kept.  The number had to be rounded off to the nearest hundreds place to keep only two significant digits.  The measurement that limited the problem to two significant digits was 5.4 cm. 

Remember that zeros are not counted as significant digits when they are to the left of the decimal place. 

Record the volume of the box, the cylinder, and the sphere to the correct significant digits, do not forget to include the units!

Cube ________________ Cylinder: ________________ Sphere: ______________

MS 095 • Lee Ling • COMFSM

Copyright ©2003 College of Micronesia-FSM.
Laboratory revised: 29 August 2000; 01 February 2003