 Part Two
Part TwoThe number of footsteps for ten Mondays as recorded by a clip on pedometer are shown in the table.
| Monday Footsteps |
|---|
| 9972 |
| 7777 |
| 8412 |
| 9307 |
| 6974 |
| 9647 |
| 8881 |
| 6866 |
| 6575 |
| 10175 |
For the number of footsteps on the ten Mondays above:
| Bins | Frequency | Relative Frequency f/n |
|---|---|---|
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| Sums: | _________ | _________ |
 Part Two
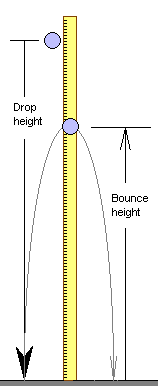
Part TwoA golf ball was dropped from increasing heights and the bounce height for the first bounce was recorded. For example, when dropped from a height of 132 centimeters, the golf ball bounced back up 107 centimeters on the first bounce. The following table includes all of the data measurements.
| Drop height/cm | Bounce height/cm |
|---|---|
| 0 | 0 |
| 41 | 33 |
| 71 | 56 |
| 132 | 107 |
| 163 | 124 |
| 193 | 147 |
| 254 | 191 |
| Basic Statistics | |||
|---|---|---|---|
| Statistic or Parameter | Symbol | Equations | Excel |
| Square root | =SQRT(number) | ||
| Sample size | n | =COUNT(data) | |
| Sample mean | x | Sx/n | =AVERAGE(data) |
| Sample standard deviation | sx or s | =STDEV(data) | |
| Sample Coefficient of Variation | CV | 100(sx/x) | =100*STDEV(data)/AVERAGE(data) |
| Linear Regression Statistics | |||
|---|---|---|---|
| Statistic or Parameter | Symbol | Equations | Excel |
| Slope | b | =SLOPE(y data, x data) | |
| Intercept | a | =INTERCEPT(y data, x data) | |
| Correlation | r | =CORREL(y data, x data) | |
| Coefficient of Determination | r2 | =(CORREL(y data, x data))^2 | |
| Statistic or Parameter | Symbol | Equations | Excel |
|---|---|---|---|
| Normal Statistics | |||
| Calculate a z value from an x | z | = |
=STANDARDIZE(x, µ, s) |
| Calculate an x value from a z | x | = s z + µ | =s*z+µ |
| Calculate a t-statistic (t-stat) | t | 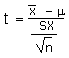 |
=(x - µ)/(sx/SQRT(n)) |
| Calculate an x from a z | =µ + zc*sx/sqrt(n) | ||
| Find a probability p from a z value | =NORMSDIST(z) | ||
| Find a z value from a probability p | =NORMSINV(p) | ||
| Confidence interval statistics | |||
| Degrees of freedom | df | = n-1 | =COUNT(data)-1 |
| Find a zc value from a confidence level c | zc | =ABS(NORMSINV((1-c)/2)) | |
| Find a tc value from a confidence level c | tc | =TINV(1-c,df) | |
| Calculate an error tolerance E of a mean for n >= 30 using sx | E | =zc*sx/SQRT(n) | |
| Calculate an error tolerance E of a mean for n < 30 using sx. Can also be used for n >= 30. | E | =tc*sx/SQRT(n) | |
| Calculate a confidence interval for a population mean µ from a sample mean x and an error tolerance E | x-E<= µ <=x+E | ||
| Hypothesis Testing | |||
| Calculate t-critical for a two-tailed test | tc | =TINV(a,df) | |
| Calculate a p-value from a t-statistic | p | = TDIST(ABS(tstat),df,#tails) | |