MS 150 Statistics Quiz 12 Fall 2004 • Name: _______________

1 to 4: Matching: Levels of Measurement

____ 1. Grades: A, B, C, D, FA. Nominal
____ 2. Favorite soy sauce: Angostura, Kikkoman, Sanbushi, Yamasa B. Ordinal
____ 3. Year: 1981, 1987, 1999, 2002C. Interval
____ 4. Soy sauce bottle volumes: 500ml, 1000ml, 1800ml D. Ratio

The table is of retail prices for 1000 ml soy sauce on Pohnpei on 04 September 2002

StoreBrandPrice
NakasoneSanbushi2.60
Wall MartKikkoman3.27
YoshieKikkoman3.45
Palm TerraceKikkoman3.69
AmbrosKikkoman3.85
Best BuyKikkoman3.89
JosaiahKikkoman3.90
Ace CommercialYamasa3.95
NakasoneKikkoman3.97
4TYYamasa4.25
PanueloYamasa4.75
En's Seven StarYamasa4.95
  1. ______ What is the sample size n?
  2. ______ What is the minimum value in this data set?
  3. ______ What is the maximum value in this data set?
  4. ______ What is the range for this data?
  5. ______ Divide the data into five bins. What is the width of a single bin?
  6. Determine the frequency and calculate the relative frequency using five bins. Record your results in the table provided.
BinsFrequencyRelative Frequency
_____________________
_____________________
_____________________
_____________________
_____________________
Sum: ______________

Hypothesis Testing Using Confidence Intervals

Sunday evening I ran 14 laps of the track with a mean lap time of 2.59 minutes and standard deviation of 8.00 seconds. Construct a 95% confidence interval using a student's t-distribution for my population mean lap time.

  1. The confidence interval for the population mean holding force of their hands µ is:
    _________ ≤ µ ≤ _________
  2. _________ On 28 December 2002 I ran an average lap time of 2.65 minutes. Was my Sunday evening lap time statistically significantly different than that of two years ago?
  3. _________ Statistically speaking, can I say I was faster?
  4. _________ What is the level of significance for this test?
  5. If this were a hypothesis test where the null hypothesis was that of no lap time difference, would we:
    1. _________ Reject the null hypothesis
    2. _________ Fail to reject the null hypothesis
  6. _________ What is the p-value?
Confidence interval statistics
Find a tc value from a confidence level c and sample size n tc   =TINV(1-c,n-1)
Calculate an error tolerance E of a mean for any n ≥ 5 using sx. E error_tolerance_tc.gif (989 bytes) =tc*sx/SQRT(n)
Calculate a confidence interval for a population mean µ from a sample mean x and an error tolerance E   x-E≤ µ ≤x+E  
Hypothesis Testing
Degrees of freedom df = n-1 =COUNT(data)-1
Calculate a t-statistic (t) t 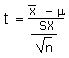xbartot (1K) (x - µ)/(sx/sqrt(n))
Calculate t-critical for a two-tailed test tc =TINV(α,df)
Calculate a p-value from a t-statistic t p = TDIST(ABS(t),df,#tails)