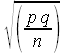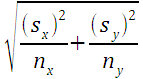Steps • Name:

Data
StudentSteps
Gabriel7095
Layoleen6593
MJ Marcus4151
Sabias6793
Alex5036
Elsihmer5404
Misty3922
Mairalinda4361
Ernest Junior5091
Lyllone3042
AllyJean4236
Felix Junior1424
Mark8966
Mersein7402
Mayoleen7618

Part I: Basic Statistics

During this term many of you have had a chance to wear a pedometer and to count your steps. Focusing the final examination on statistics from pedometers seems like a natural way to end this term. The data in the table comes from pedometers worn by second grade students at Rural Elementary School (RES). The data is the daily average steps for each of the students.

Data sheet

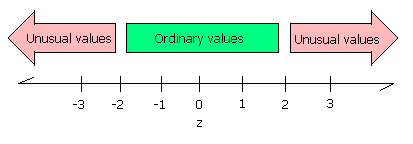
  1. _________ What level of measurement is the data?
  2. _________ Determine the sample size n.
  3. _________ Determine the minimum.
  4. _________ Determine the maximum.
  5. _________ Calculate the range.
  6. _________ Calculate the midrange.
  7. _________ Determine the mode.
  8. _________ Determine the median.
  9. _________ Calculate the sample mean x.
  10. _________ Calculate the sample standard deviation sx.
  11. _________ Calculate the sample Coefficient of Variation.
  12. _________ Determine the bin width. Use five classes (bins or intervals).
  13. Fill in the following table with the class upper limits in the first column, the frequencies in the second column, and the relative frequencies in the third column
Bins (x)Frequency fRF p(x)
Sums:
  1. Sketch a histogram of the relative frequency data.
  2. __________________ What is the shape of the distribution?
  3. __________________ Use the sample mean x and sample standard deviation sx above to calculate the z-score for first grader Shana who averages 8840 steps per day.
  4. _________ Is the z-score for Shana an ordinary or extraordinary value?
  5. __________________ Use the sample mean x and sample standard deviation sx above to calculate the z-score for second grader Marlin who averages 11811 steps per day.
  6. _________ Is the z-score for Marlin an ordinary or extraordinary value?
  7. _________ Calculate the standard error of the sample mean x for the number of steps.
  8. _________ Find tcritical for a confidence level c of 95% for the number of steps.
  9. _________ Determine the margin of error E for the sample mean x.
  10. Write out the 95% confidence interval for the population mean μ number of steps:
    p(_____________ < μ < ___________) = 0.95
  11. _________ The population mean number of steps μ for the Urban Elementary School (UES) second graders is 6246 steps per day. Is this a possible population mean for the Rural Elementary School (RES) students?
  12. _________ Are the UES students statistically significantly more active than the RES students as measured by steps per day?

Part II: Hypothesis Testing using the t-test

A study was conducted to determine differences in the number of steps between the rural Rural Elementary School (RES) students and the Urban Elementary School (UES) students. The data in the table is the average daily steps for the students.

Steps
RES studentsSteps (x) UES studentsSteps (y)
Gabriel7095Frankie16269
Layoleen6593Shawna3712
MJ Marcus4151Alan9713
Sabias6793Danielle6293
Alex5036Kevin9529
Elsihmer5404Rejazy3747
Misty3922Alexandra1019
Mairalinda4361Marlin9669
Ernest Junior5091Anjelu2914
Lyllone3042AJ3798
AllyJean4236Arianne1823
Felix Junior1424Burt4482
Mark8966Aiyumi7095
Mersein7402Trumaine4071
Mayoleen7618Vincent7616
Faith4123
Hart10068
Kelsey3309
Hagadauroma8828
Beatrice6840
  1. _________ Calculate the sample mean x average daily steps for Rural Elementary School (RES).
  2. _________ Calculate the sample mean y average daily steps for Urban Elementary School (UES).
  3. _________ Are the sample means for the two samples mathematically different?
  4. _________ Calculate the degrees of freedom using the smaller of the two sample sizes.
  5. _________ Calculate the tcritical using alpha α = 0.05 and the degrees of freedom.
  6. _________ Calculate the standard error SE for two independent samples.
  7. _________ Calculate the margin of error E for two independent samples.
  8. ____________ < μd < _____________ Determine the 95% confidence interval for the population mean difference μd
  9. _________ Does the confidence interval include a mean difference of zero?
  10. __________________ What is the p-value? Use the difference of means for independent samples TTEST function =TTEST(data_range_x;data_range_y;2;3) to determine the p-value for this two sample data.
  11. __________________ Is the difference in the mean daily steps statistically significant at a risk of a type I error alpha α = 0.05?
  12. __________________ Would we "fail to reject" or "reject" a null hypothesis of no difference in the steps per day between the two schools?
  13. __________________ What is the maximum level of confidence we can have that the difference is statistically significant?

Part III: Linear Regression (best fit or least squares line)

Cadence versus speed
Cadence (steps/min)Speed (cm/s)
148.0234
150.0250
151.3239
151.4239
152.4250
153.2224
153.6256
154.7250
154.8235
155.4290
155.4240
155.5276
159.3245
159.7248

The data in this section explores the relationship between cadence (steps per minute) and speed (centimeters per second). In distance running theory, the optimal cadence is up around 180 steps per minute. This should produce the highest sustainable speed for distance running. As a joggler, my cadence is synchronized to my juggling. This section of the examination explores whether my cadence as measured by a pedometer is related to my speed as measured by a global positioning satellite receiver.

  1. _________ Calculate the slope of the linear regression (best fit line).
  2. _________ Calculate the y-intercept of the linear regression (best fit line).
  3. _________ Is the relation between cadence and speed positive, negative, or neutral?
  4. _________ Calculate the linear correlation coefficient r for the data.
  5. ______________ Is the correlation none, weak/low, moderate, strong/high, or perfect?
  6. _________ Use the slope and intercept to predict the speed for a cadence of 149 steps per minute.
  7. _________ Use the slope and intercept to determine the cadence produced by a speed of 200 cm/s.

One intention of any course is that a student should be able to learn and employ new concepts in the field even after the course is over. In a linear regression analysis a correlation coefficient near zero means no relation exists between the variables. You can run a statistical test to determine whether the correlation coefficient r is statistically signigicantly different from zero. If the difference of r from zero is statistically significant, then you will have proved that a relationship exists. If you fail to reject a null hypothesis of r equals zero, then there is no evidence in the data that cadence and speed are linked.

To run the hypothesis test, you will calculate a t-critical (tc), a t-statistic (t), and then a p-value using the t-statistic and the TDIST function.

For this test:
sample size n is the number of data pairs
t-critical: =TINV(α;n−2) where α = 0.05
t-statistic = r n − 2 1 − r 2
p-value: =TDIST(ABS(t-statistic);n−2;2)

Note that n−2 is used in these formulas. This is the degrees of freedom for a correlation hypothesis test.

  1. _________ Determine the sample size n by counting the number of data pairs.
  2. _________ Determine t-critical using an alpha of α = 0.05 and n − 2 degrees of freedom.
  3. _________ Determine the t-statistic using the formula noted further above, remembering to use n − 2 for the degrees of freedom.
  4. _________ Determine the p-value using the TDIST function, remembering to use n − 2 for the degrees of freedom.
  5. ________ Is the correlation between my cadence and my speed statistically significant?

Tables of Formulas and OpenOffice Calc functions

Basic Statistics
Statistic or ParameterSymbolEquationsOpenOffice
Square root=SQRT(number)
sample size nn=COUNT(data)
sample mean x Σx/n =AVERAGE(data)
Sample standard deviationsx or s=STDEV(data)
Sample Coefficient of VariationCV sx / x =STDEV(data)/AVERAGE(data)
Formula to calculate a z value from an x value z z-score from a sample mean =STANDARDIZE(x;x;sx)
Confidence interval statistics for a single sample
Statistic or ParameterSymbolEquationsOpenOffice
Sample sizenn=COUNT(data)
Degrees of freedomdfn − 1=COUNT(data)-1
Find a tcritical value from a confidence level c tc =TINV(1-c;df)
Standard error of a sample mean x SE standard error) =STDEV(data)/SQRT(n)
Standard error of a sample proportion p SE se_proportion =SQRT(p*q/n)
Calculate a margin of error for the mean E using tcritical and the standard error SE. E margin_error =tc*SE
Calculate a confidence interval for a population mean μ from a sample mean x and a margin of error E x - E < μ < x + E
Calculate a confidence interval for a population proportion P from a sample proportion p and a margin of error E p - E < P < p + E
Hypothesis testing for a sample mean versus a known population mean
Statistic or ParameterSymbolEquationsOpenOffice
Relationship between confidence level c and alpha α for two-tailed tests 1 − c = α
Calculate t-critical for a two-tailed test tc=TINV(α;df)
Calculate a t-statistic t t-statistic =(x - μ)/(sx/SQRT(n))
Calculate a two-tailed p-value from a t-statisticp-value = TDIST(ABS(t);df;2)
Hypothesis testing for paired data samples
Statistic or ParameterSymbolEquationsOpenOffice
Calculate a p-value for the difference of the means from two samples of paired data =TTEST(data_range_x;data_range_y;2;1)
Hypothesis testing and confidence intervals for two independent samples
Statistic or ParameterSymbolEquationsOpenOffice
Degrees of freedom (approx.)df [smaller sample n] − 1=COUNT(smaller sample)-1
Calculate t-critical for a two-tailed test tc=TINV(α;df)
Calculate the standard error SE for two independent samples SE standard error for two sample means =sqrt((sx^2/nx)+(sy^2/ny))
Calculate a margin of error E for two independent samples using tcritical and the standard error SE. E margin_error =tc*SE
Calculate the difference between two sample means xd x − y =average(data set x)-average(data set y)
Calculate a confidence interval for a population mean difference μd from a sample mean difference xd and a margin of error E xd − E < μd < xd + E
Calculate a p-value for the difference of the means for two independent samples (data unpaired, independent) where the population standard deviations are unknown =TTEST(x data;y data;2;3)
Linear regression statistics
Statistic or ParameterSymbolEquationsOpenOffice
Slopeb=SLOPE(y data; x data)
Intercepta=INTERCEPT(y data; x data)
Correlationr=CORREL(y data; x data)
Coefficient of Determinationr2 =(CORREL(y data; x data))^2

Z-scores diagram

Statistics • Courses • COM-FSM