
This page displays colors using the hue, saturation, and luminosity module of CSS. Browsers that fully support this module are necessary to display this page. As of 2005, FireFox supports this module, Microsoft Internet Explorer does not.
The support for the Hue-Saturation-Luminosity module (HSL) in Cascading Style Sheets (CSS) allows the exploration of the colors of the rainbow from a mathematical perspective. In the HSL model, hues are specified by an angular measure. The primary colors of light are red, green, and blue. In the HSL model red is at 0°, green is at 120°, and blue is at 240°. The secondary colors of light are located at half the primary angles. Yellow is at 60°, cyan at 180°, and magenta is at 270°.
In Micronesia many of the local languages have only four color words applicable to the rainbow, typically red, yellow, green, and blue. This rainbow would appear as follows:
| red hsl(0,100%,50%) |
| yellow hsl(60,100%,50%) |
| green hsl(120,100%,50%) |
| blue hsl(240,100%,50%) |
An "equiangular" four color rainbow would be:
| red hsl(0,100%,50%) |
| yellow-green hsl(90,100%,50%) |
| cyan hsl(180,100%,50%) |
| purple hsl(270,100%,50%) |
A drawing of a rainbow by a child rainbow often has six colors, and this is arguably the most easily identified colors for English speakers in the rainbow:
| red hsl(0,100%,50%) |
| orange hsl(30,100%,50%) |
| yellow hsl(60,100%,50%) |
| green hsl(120,100%,50%) |
| blue hsl(240,100%,50%) |
| purple hsl(270,100%,50%) |
Although the above is visually a rainbow, the angular distribution is not equiangular. An equiangular six-color rainbow could be, among other rotations, the primary and secondary colors:
| red hsl(0,100%,50%) |
| yellow hsl(60,100%,50%) |
| green hsl(120,100%,50%) |
| cyan hsl(180,100%,50%) |
| blue hsl(240,100%,50%) |
| magenta hsl(300,100%,50%) |
Sir Isaac Newton gave the rainbow seven colors. Some have argued that he was influenced by his religious background in which six was an inauspicious number while seven was considered a "complete" and holy number. Young children usually know the six colors described above, but the seventh color, "indigo", is usually a mystery. The HSL model provides a way to tackle the mystery mathematically. Blue is clearly at 240° and red returns at 360°. This puts indigo and violet in between blue and red. Using equiangular mathematics, indigo could be at 240° + 40° and violet could be at 240° + 40° + 40°:
| red hsl(0,100%,50%) |
| orange hsl(30,100%,50%) |
| yellow hsl(60,100%,50%) |
| green hsl(120,100%,50%) |
| blue hsl(240,100%,50%) |
| indigo hsl(280,100%,50%) |
| violet hsl(320,100%,50%) |
Although the above does not look quite right, the representation of a purple band inside a magenta or violet band is not wholly inaccurate for a rainbow.
What would a seven color equiangular rainbow look like? If one starts at 0°, and one need not necessarily do so, the result is (colors borrowed from nearest x11 color):
| red hsl(0,100%,50%) |
| gold hsl(51,100%,50%) |
| chartreuse hsl(103,100%,50%) |
| spring green hsl(154,100%,50%) |
| dodger blue hsl(206,100%,50%) |
| saturated slate blue hsl(257,100%,50%) |
| deep pink - violet, arguably fuchsia hsl(309,100%,50%) |
A digital image of a Pohnpeian rainbow was analyzed for some insight into the possible optimal choices for a rainbow color set. The data set, however, can only provide broad guidance as the response characteristics of the digital imaging electronics vary greatly from that of the human eye. These differences are likely to be most pronounced when dealing with what are effectively slices of monochromatic light produced by a rainbow. The rainbow was shot againt a somewhat neutral gray cloudy sky and then balanced to bring up the saturation and luminosity without shifting the underlying color angles.

A slice was taken through the original image and rotated. The slice at 400%:

Of interest in the image is the clear existence of colors noted above, including the equiangular colors such as cyan. Leaving out "blends" such as red-orange and yellow-orange, one can identify the presence of red, orange, yellow, green, cyan, blue, purple, and magenta tones. With blends there are certainly and obviously more colors. This opens up the question of the value of having students memorize the seven hues of the Newtonian rainbow, the "ROYGBIV" memorization. Ultimately the ability to name the Newtonian rainbow colors is meaningless, and the issue of the true color of indigo is rendered moot.
After looking at the pixel rows visually, pixel row 19 was selected traversed. This decision was rather arbitrary. Here is row 19 at 500% horizontally and 1500% vertically:
![]()
Using GIMP 2.2 to analyze the pixels for hue angle yielded the following for the central colored bands in the image:
![]()
There are a number of interesting features. The rate of hue angle change is not constant as one moves from left to right. Change is slow at first, speeds up around 90 pixels at a hue angle of about 100°, and then slows down again around pixel 120 at a hue angle of about 225°.
Progressing from left to right there does exist a hue angle of nearly zero (pure red) around pixel 32, but the saturation and lumninosity are remarkably low, especially in row 19. Thus red exists, but is very dim. While the rainbow traditionally starts with red, the pixels to the left of the 32nd pixel have color angles from 346° to 358°. These are colors between magenta and red, low luminosity red-violets that can be seen as dark pinkish-purple splotches first image. Thus the rainbow starts not with red but with red-violets out beyond 270°.
The steady progression from left to right means that all hues are present, but there are variations in saturation and luminosity that make the progression appear less even to the eye. At the resolution of a single pixel many factors may contribute to these variations in saturation and luminosity.
The digital imaging chip may not have a linear response at each and every hue angle. Rain in the atmosphere or dust on the lens could conceivably impact the saturation and luminosity of a single pixel. Luminosity and saturation were not studied to look for patterns of reduced sensitivity in particular hue ranges. The inherent non-linearity in the progression suggests that either rainbow hues are non-linear with respect to the hue angle progression or the digital imaging chip responds in a non-linear manner.
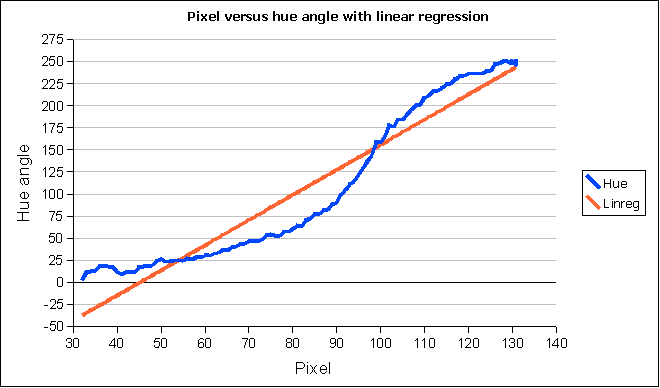
Suppose one wanted to pick seven colors to represent the rainbow. What colors would the image suggest selecting? The distribution of hues was determined for seven equal intervals from pixel 32 with a hue angle of 2° and pixel 131 with a hue value of 252°. Note that the 252° value came from pixel row six, the row 19 value was 246°. The choice of the value in pixel row six (first image) was due solely to that being the largest angle found on the right side of the image. Note that there might be an "inverted" rainbow just inside the primary bow that represents a larger number of internal reflections. The hue angles beyond pixel 131 rapidly collapsed back into low luminosity blue-greens, with angles as low as 190° by pixel 145. Unsure what to do with the "high" hue angles to the right of pixel of 32, the histogram includes only the more obvious red to purple core of the rainbow. The relative frequencies also indicate the non-linear distribution in the non-uniform relative frequencies.
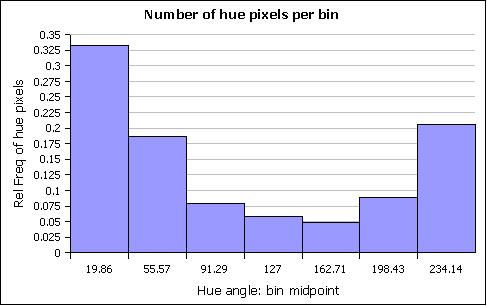
Dividing up the pixel range from 32 to 131 pixels into seven hues with endpoints at 32 pixels and 131 pixels, one obtains the following "rainbow" (color names borrowed from nearby x11 colors):
| red hsl(2,80%,50%) |
| orange-red hsl(24,100%,50%) |
| orange-yellow hsl(39,100%,50%) |
| yellow-tinged green hsl(70,100%,50%) |
| aquamarine hsl(158,100%,50%) |
| royal blue hsl(230,70%,50%) |
| medium purple hsl(252,100%,70%) |
Note that hsl(252,100%,50%) is clearly a blue tone, while the image shows the same hue to be a lavender purple [hsl(252,100%,70%)]. This is the result of the impact of luminosity. After making this adjustment, two other colors were also tweaked to closer approximate the original digital image. The 252° hue angle provides an interesting look at the impact of saturation and luminosity:
| hsl(252,20%,10%) | hsl(252,40%,10%) | hsl(252,60%,10%) | hsl(252,80%,10%) | hsl(252,100%,10%) | hsl(252,60%,10%) | hsl(252,80%,10%) | hsl(252,100%,10%) |
| hsl(252,20%,20%) | hsl(252,40%,20%) | hsl(252,60%,20%) | hsl(252,80%,20%) | hsl(252,100%,20%) | hsl(252,60%,20%) | hsl(252,80%,20%) | hsl(252,100%,20%) |
| hsl(252,20%,30%) | hsl(252,40%,30%) | hsl(252,60%,30%) | hsl(252,80%,30%) | hsl(252,100%,30%) | hsl(252,60%,30%) | hsl(252,80%,30%) | hsl(252,100%,30%) |
| hsl(252,20%,40%) | hsl(252,40%,40%) | hsl(252,60%,40%) | hsl(252,80%,40%) | hsl(252,100%,40%) | hsl(252,60%,40%) | hsl(252,80%,40%) | hsl(252,100%,40%) |
| hsl(252,20%,50%) | hsl(252,40%,50%) | hsl(252,60%,50%) | hsl(252,80%,50%) | hsl(252,100%,50%) | hsl(252,60%,50%) | hsl(252,80%,50%) | hsl(252,100%,50%) |
| hsl(252,20%,60%) | hsl(252,40%,60%) | hsl(252,60%,60%) | hsl(252,80%,60%) | hsl(252,100%,60%) | hsl(252,60%,60%) | hsl(252,80%,60%) | hsl(252,100%,60%) |
| hsl(252,20%,70%) | hsl(252,40%,70%) | hsl(252,60%,70%) | hsl(252,80%,70%) | hsl(252,100%,70%) | hsl(252,60%,70%) | hsl(252,80%,70%) | hsl(252,100%,70%) |
| hsl(252,20%,80%) | hsl(252,40%,80%) | hsl(252,60%,80%) | hsl(252,80%,80%) | hsl(252,100%,80%) | hsl(252,60%,80%) | hsl(252,80%,80%) | hsl(252,100%,80%) |
| hsl(252,20%,90%) | hsl(252,40%,90%) | hsl(252,60%,90%) | hsl(252,80%,90%) | hsl(252,100%,90%) | hsl(252,60%,90%) | hsl(252,80%,90%) | hsl(252,100%,90%) |
| hsl(252,20%,95%) | hsl(252,40%,95%) | hsl(252,60%,95%) | hsl(252,80%,95%) | hsl(252,100%,95%) | hsl(252,60%,95%) | hsl(252,80%,95%) | hsl(252,100%,95%) |
The complexity that saturation and luminosity bring to a single hue angle reaffirms the sense that there is no "right" number of colors in the rainbow. There is a definite sequence to any particular system of colors, but no singularly correct sequence. In a world dominated by RGB color reproduction systems such as color televisions and monitors, there may be a logic in using the primary and secondary colors of light, which visually appears best when sequenced red, yellow, green, cyan, blue, purple, magenta. Although magenta is present beyond red, the luminosity and saturation are so low as to rarely be visible to the naked eye. Magenta looks better placed beyond purple. This creates an eight color rainbow. The eight color rainbow is not only not equiangular, but - as in the graphs above - tends to move more "slowly" through red orange and yellow and then more "quickly" through the "higher" angles.
| red hsl(0,100%,50%) |
| orange hsl(30,100%,50%) |
| yellow hsl(60,100%,50%) |
| green hsl(120,100%,50%) |
| cyan hsl(180,100%,50%) |
| blue hsl(240,100%,50%) |
| purple hsl(270,100%,50%) |
| magenta hsl(300,100%,50%) |
The above, if fanciful, also reflects the inherent circularity of colors wherein purple, magenta, red-violets, and deep pinks are part of the transition from blue to red.