This document is rough and not particulary ready for prime time. This reflects fairly raw notes. This document uses the Symbol font. Absence of this font will cause fairly serious readability problems.
A set is a group formed by a classification, a well-defined collection of objects.
The members of a set are called the elements of the set.
Here we are using the English meaning of set as a grouping: a set of spoons, a dining room set.
Well-defined sets:
Not well defined:
All of these are vaguely defined because they involve opinion and judgement.
Venn diagrams can assist in the analysis of sets. Venn diagrams were named for the mathematician John Venn.
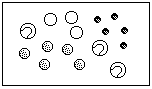
The Universal set is the set of all elements under consideration. The Universal set in a Venn diagram is drawn as a rectangle. A Universal set consisting of all the spheres on the table would be drawn:

Sets are enclosed using bracket symbols: { }
The set could be written U = {marble, ping pong, tennis, superball, wiffle}
with each element separated by a comma from the other elements. Often lower case letters are used as abbreviations for elements of a set:
U = {m, p, t, s, w}
There is a special symbol for a set that has no elements. A set with no elements is called an empty set. The symbol for an empty set is {} or, alternatively, ∅.
The set of all cars in Mokil is an empty set: there are no cars in Mokil.
This would be written: {}
Sets made up of some or all of the elements in the Universal set are called subsets.
On a large rectangular table is a collection of balls and marbles.
Let U = {x|x is a sphere on the table}
The ping pong balls would be a subset of this Universal set. This would be written:
{ping pong balls} ⊆ U or {ping pong balls} ⊆ {spheres on the table}
In a Venn diagram a circle would be drawn around the ping pong balls, in class a circle of yarn is placed around the balls for each example and a diagram is drawn on the board.
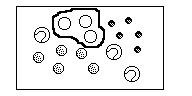
Sample board diagram: ping pong ball subset.
Another subset would be the set of all white balls.
Another subset would be the set of all hollow balls.
The set of all the balls would also be a subset of the balls. That is, a subset can be a smaller set or an equivalent set to the larger set, hence the symbol ⊆ . The "larger" set is sometimes called the superset.
A set which does not contain all of the members of the larger superset is called a proper subset. The set of ping pong balls is a proper subset. The set of white balls is a proper subset. The set of hollow balls is a proper subset.
The symbol ⊂ is used for a proper subset.
Let U = {all spheres on the table}
{ping pong balls} ⊂ U
{white balls} ⊂ U
{hollow balls} ⊂ U
What is the set of all basketballs on the table? There are no basketballs, thus the set is an empty set, {}. This would be represented by placing a circle around none of the balls on the table. The empty set is a subset of all sets.
Add children's letter cubes to the table:
Note that {letter cubes} ⊄ {spheres on the table} because cubes are not spheres.
Consider an empty set. How many subsets are there of the empty set?
One. All sets include an empty set subset, even the empty set.
The empty or null set has only itself as a subset:
{ } ⊆ { } 1 empty set subset
Consider a set containing a single tennis ball. How many subsets does it have?
A Universal set with one element (a tennis ball) has:
U = {t}
{ } ⊆ {t} 1 1 null set subset
{t} ⊆ {t} 1 1 single element subset
2 subsets of a 1 member universal set.
A set with two elements, a tennis ball and a ping pong ball, U = {t, p} has:
{ } ⊆ {t, p} 1 null set subset
{t} ⊆ {t, p} {p} ⊆ {t, p} 2 single element subsets
{t,p} ⊆ {t,p} 1 two element subset
4 subsets of a 2 element universal set
The following exercise was done by the students working in groups with an actual tennis ball, pingpong ball, and superball.
U = {tennis, ping pong, superball} = {t, p, s}
{} ⊆ {t,p,s} 1 null set subset
{t} ⊆ {t,p,s} {p} ⊆ {t,p,s} {s} ⊆ {t,p,s} 3 single element subsets
{t,p} ⊆ {t,p,s} {p,s} ⊆ {t,p,s} {t,s} ⊆ {t,p,s} 3 two element subsets
{t,p,s} ⊆ {t,p,s} 1 triple element subset
8 subsets of a 3 element universal set
Results of the above were posted to the board. The next exercise was done by the students working in groups with an actual tennis ball, pingpong ball, superball, and a marble.
U = {tennis, ping pong, superball, marble} = {t, p, s, m}
{∅} ⊆ {t,p,s,m} 1 null set subset
{t} {p} {s} {m} 4 single element subsets
{t,p} {t,s} {t,m} {p,s} {p,m} {s,m} 6 two element subsets
{t,p,s} {t,s,m} {t,p,m} {p,s,m} 4 three element subsets
{t,p,s,m} 1 four element subset
16 subsets of a 4 element universal set
In class group activity:
Work in groups of four to determine the number of subsets of a five element set. Appoint one person a recorder, list each of the subsets and then count them.
U = {tennis, ping pong, superball, marble, fuzzy pompom} = {t, p, s, m, f}
{∅} ⊆ {t,p,s,m} __ null set subsets
{t} {p} {s} {m} {f} __ single element subsets
__ two element subsets
__ three element subsets
__ four element subsets
__ five element subsets
HW: How many total subsets are there for a six element set?
Consider the sequence:
1 1 1 1 1 1
1 2 3 4 5
1 3 6 10
1 4 10
1 5
1
1 2 4 8 16 32
Turn the sequence sideways to get:
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1
And then spread it out as shown below:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
The pyramid is called Pascal's Triangle.
Add each row of Pascal's Triangle:
1 = 1
1 + 1 = ___
1 + 2 + 1 = ___
1 + 3 + 3 + 1 = ___
1 + 4 + 6 + 4 + 1 = ___
1 + 5 + 10 + 10 + 5 + 1 = ___
Use a calculator to calculate the following results. On a scientific calculator the yx key or the xy key does exponents.
20 = ___
21 = ___
22 = 2 × 2 = ___
23 = 2 × 2 × 2 = ___
24 = 2 × 2 × 2 × 2= ___
25 = 2 × 2 × 2 × 2 × 2 = ___
Pascal's Triangle appears in many places. Use the yx key or the xy key on your calculator to do the following:
110 =
111 =
112 =
113 =
114 =
The intersection of two sets is the set of all elements in common to the two sets. The symbol for intersection is ∩ .
The intersection of the set of hollow spheres and the set of white balls are those elements that are in both circles of yarn (as demonstrated in class on the table).
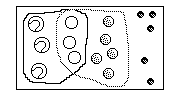
Thus {white spheres} ∩ {hollow spheres} = {pingpong balls}
This could be written with symbols:
This could be written with symbols:
W = {white spheres} = {pingpong, golf balls}
H = {hollow spheres} = {tennis, pingpong}
P = {pingpong balls}
Thus:
W ∩ H = P
Using G = {Golf balls}
M = {Marbles}
P = {Ping pong balls}
T = {neon color Tennis balls}
Then the Universal set could be written U = {G, M, P, T}
More examples:
{solid spheres} ∩ {the spheres for which the game can be played indoors} = {marbles}
{fuzzy spheres} ∩ {solid spheres} = {} = ∅ There are no solid fuzzy balls.
{the vowels} ∩ {the first five letters of the alphabet} =
{a,e}
(the vowels} ∩ {the letters in "rhythm"} = {} = ∅ There are no vowels in rhythm.
The intersection of the positive even numbers and the prime numbers has a single element:
{positive even numbers} ∩ {prime numbers} = {2}
Thus, given a set A and a set B:
A ∩ B = {x|x ∈ A and x ∈ B}
"A intersection B is any element such that the element x is an element in set A and an element in set B"
Example:
Given A = {x|x is a positive odd number less than 1000}
and B = {x|x is a positive perfect cube}
Then A ∩ B = {27, 125, 343, 729}
HW
On a table is a collection of spheres.
Let G = {white Golf balls}
M = {colored Marbles}
P = {white Ping pong balls}
T = {neon color Tennis balls}
W = {White spheres}
H = {Hollow spheres}
S = {Solid spheres}
I = {spheres used in Indoor games}
Ou = {spheres used in Outdoor games}
Sm = {Smooth spheres}
Write out the elements of the following intersections as sets:
Example: O ∩ H Solution: {tennis balls} or {T}
1. S ∩ W
2. H ∩ Ou
3. H ∩ S
4. Is T ∈ H ∩ W?
Write out the set that results from the following intersections:
5. A = {x|x is a positive even number less than 200}
B = {x|x is a positive perfect square}
6. Determine the number of three element subsets of a seven element Universal
set.
7. Determine the number of ways to obtain three heads and four tails on seven pennies.
8. Determine the binomial expansion (x + 1)7
The union of two sets is the set of all elements that are in either set.
The union of the white spheres and the hollow spheres would be:
W ∪ H = {T, P, G} = {Tennis, Ping pong, Golf}
The union includes everyone in both yarn circles.
A = {x|x is an odd integer less than twenty}
B = {x|x is a perfect square less than twenty}
A = {1,3,5,7,9,11,13,15,17,19}
B= {1,4,9,16}
A ∪ B = {1,3,4,5,7,9,11,13,15,16,17,19)
Note that A ∩ B = {1,9}
In concrete object set theory removal involves calculating what was not in the intersection of the sets.
{golf, marble, marble, pingpong, pompom } remove {marble, pingpong} involves the following diagram:

In the intersection of the two sets diagrammed is {marble, pingpong}. The result of the removal are those elements that are not in the intersection. A removal symbol was used: a slash bar through an intersection symbol when set theory removal was done. Note that removal is sufficiently complex that no standard font set even includes this bizarre beast (the elements that are not in the intersection).
Title III Math/Science Software Specialist
College of Micronesia-FSM
Notebook material first developed 1994 at the College of Micronesia - FSM. For further information on this project, contact dleeling@comfsm.fm Web page later designed and run on Micron Millenia P5 - 133 MHz with 32 MB RAM, Windows 95 OS. Edited in 2011 to shift from the use of font tags and the Symbol font to unicode code points. 2011 work done on an Intel(R) Celeron(R) CPU 3.06GHz with 2045MB (339MB used) running the Ubuntu 11.10 distribution on Linux 3.0.0-14-generic (i686) under the LXDE (Lubuntu) desktop environment.