mb2 SVG day one

Over the next couples of days the models focus on web page creation using Scalable Vector Graphic (SVG) extensions to HTML5. This is the cutting and bleeding edge of web page design. You will be using trigonometry to lay out some basic shapes on a 200 by 200 grid with these technologies. These skills, based in mathematics, are of most use to the CIS majors. The activities also provide a vehicle for exploring the trigonometric functions.

The SVG grid is like an xy graph EXCEPT that the y-axis is UPSIDE-DOWN. To draw shapes on the grid you will use a text editor. This will be demonstrated in class. Then the pages will be opened and viewed using FireFox.

HTML5 + SVG code is composed using a text editor.

In Microsoft Windows use Notepad.exe as a text editor.
Notepad

Launch this from the "Run" dialog box in the start menu.
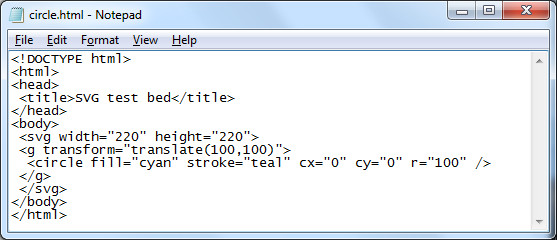
Launching Notepad

<!DOCTYPE html>
<html>
<head>
 <title>SVG test bed</title>
</head>
<body>
 <svg width="220" height="220">
 <g transform="translate(100,100)">
  <circle fill="cyan" stroke="teal" cx="0" cy="0" r="100" />
 </g>
 </svg>
</body>
</html>

HTML is very very fussy - the slightest typing error will cause the web page to fail. The center of the circle is at (cx,cy). The numbers are measurements in pixels. Pixels are "picture elements". Picture elements are the smallest controllable element of a computer monitor.

The next task is where trigonometry comes into play: we are going to draw a square in the circle. To draw the square exactly inside the circle ("inscribed") we need to determine where the corners of the circle are located. The circle has a radius r of 100. To find the coordinates of these corners we will need to work out the length of the adjacent and opposite sides of a 45° triangle. This will help us locate the corners of the 45-45-90° right triangle that is the building block of the square.

The SVG code to draw this square will have the form of...
<path fill="none" stroke="silver" d="M x1,y1 L x2,y1 x2,y2 x1,y2 x1,y1" />
where the x1,y1 elements will be replaced by numbers, by coordinate pairs.

Calculating the coordinates requires determining the length of the bases of the 45-45-90 triangle. This calculation requires using sine and cosine. The sine function, abbreviated sin, can be used to calculate the length of the side opposite the angle theta θ.

$sine (θ) = \sin (θ) = \frac{opposite}{hypotenuse} = \frac{y}{r}$

Cross multiply and one gets y = r sin(θ).
r = 100 and θ = 45°
Thus y = 100*sin(45°)

The cosine function, abbreviated cos, can be used to calculate the length of the side adjacent the angle theta θ.

$cosine (θ) = \cos (θ) = \frac{adjacent}{hypotenuse} = \frac{x}{r}$

Cross multiply and one gets y = r cos(θ). r = 100 and θ = 45° Thus y = 100*cos(45°)

For both of the above results, we will have to round off the decimal portion of the number. SVG does not use fractional pixel values. Both calculations have the same answer: 71 pixels.

The center of the circle is (0,0). This is our "starting" place. Moving to the right 71 pixels adds 71 to x-value in the (x, y) coordinate. This puts us at the right-angle corner of the triangle.

Moving up 71 pixels is moving in the negative y direction. This means we have to subtract 71 from the y value at the right-angle corner.

Thus the coordinate for the upper right hand corner is (71,-71). This will be the first coordinate in the path command that will draw our square

<path fill="none" stroke="black" d="M 71,-71 L , , , , " />

The "M" in the path attribute means "Move to..." This tells the computer where to start our SVG diagram. The "L" means "Line" as in "draw a Line to". The next step is to tell the computer where the line should go.

Let us start by going down to the lower right corner of the square. Using the same basic argument as above, the lower right corner of the square must be 100*sin(45°) below the center - that is, 71 pixels down from 0. Or 142 pixels down from the upper right corner. Each side of the square is two times 71 pixels long.

<path fill="none" stroke="black" d="M 71,-71 L 71,71 , , , " />

Using the above approach, we can work our way around the square, corner to corner, returning eventually to the upper right corner at (71,-71).

<path fill="none" stroke="black" d="M 71,-71 L 71,71 -71,71 -71,-71 71,-71" />

Square centered on (0,0):

<!DOCTYPE html>
<html>
<head>
 <title>SVG test bed</title>
</head>
<body>
 <svg width="220" height="220">
 <g transform="translate(100,100)"> 
  <circle fill="lavender" stroke="indigo" cx="0" cy="0" r="100" />
  <path fill="thistle" stroke="black" d="M 71,-71 L 71,71 -71,71 -71,-71 71,-71" />
  </g>
 </svg>
</body>
</html>

The colors used in the above HTML/SVG code come from the X11 color palette.

Equilateral triangle

Next we will tackle an equilaterial triangle. The key to solving this will be using the 30-60-90 triangle in the diagram.

Homework: Using adjacent = r cos θ and opposite = r sin θ, try to work out the coordinates of the circle at the vertices of the equilateral triangle. Note that r = 100, the center of the triangle is located at (0, 0), and the angle θ is 60°. The grid we are using is on the right.