where x is the bounce number and f(x) is the bounce height. Solve for the bounce number x where the bounce height f(x) is 64 centimeters high.
| Attempt | Time (s) |
|---|---|
| 1 | 0 |
| 5 | 8.54 |
| 9 | 12.25 |
| 16 | 16.58 |
In February 2010 my daughter wanted to learn to ride a RipStik. Recognizing the opportunity to gather data, I timed each attempt she made to ride the RipStik. Her first time on the RipStik she fell off immediately - a ride of 0 seconds. By her fifth attempt she remained on the RipStik for 8.54 seconds. The data in the table above is selected from the first 16 attempts to ride the RipStik. Plot this data using a LibreOffice.org Calc spreadsheet. Add in a logarithmic trend line. Write the natural logarithmic trend line below. Round numbers to two decimal places:
f(x) = _________ ln(x) + ____________
Where No is the initial amount of the radioactive material, r is the rate of radioactive decay, t is the time, and N is the amount left after time t. Polonium-210 is a highly radioactive substance. Polonium-210 has a half life of 138 days. After a time t of 138 days, an initial amount No of 100 nanograms will be an amount N of 50 nanograms. Use this information to solve for the radioactive decay rate constant r for Polonium-210.
r = _________________
A: ( ________ , _________ )
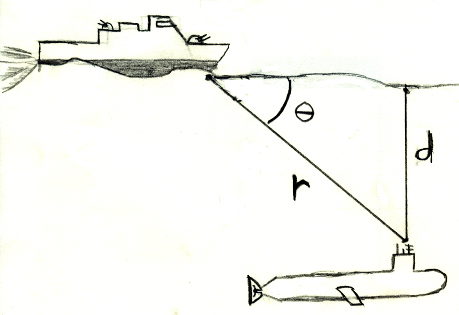 d = _________
Depth charges are explosives that detonate at a specific depth d under the surface of the water. A destroyer armed with depth charges is using a sonar to determine the angle θ and the distance r to a submarine. If the angle θ = 40° and the range r is 156 meters, what is the value of the depth d?
d = _________
Depth charges are explosives that detonate at a specific depth d under the surface of the water. A destroyer armed with depth charges is using a sonar to determine the angle θ and the distance r to a submarine. If the angle θ = 40° and the range r is 156 meters, what is the value of the depth d?λ = _______________ Write the wavelength λ for one wavelength of the RipStik swizzle wave in centimeters.
θ =
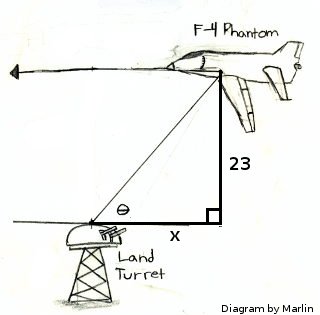
f(x) = _______________ sin( ____________ t)
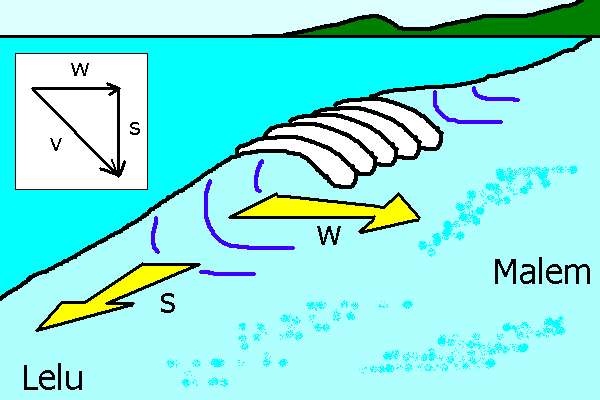 On a Thursday evening in July 2005 I was body board surfing in Malem. My total
velocity v (speed) was the result of the vector addition of the
velocity (speed) of the wave w and the velocity s of my board
along the face of the wave. On that Thursday the waves were moving at a speed of:
On a Thursday evening in July 2005 I was body board surfing in Malem. My total
velocity v (speed) was the result of the vector addition of the
velocity (speed) of the wave w and the velocity s of my board
along the face of the wave. On that Thursday the waves were moving at a speed of:towards Malem and my board was moving at
towards Lelu. Speed are in meters per second.
Note that w and s are at right angles as shown in the inset diagram.
Calculate my velocity v over the reef by adding the vectors w + s and reporting the magnitude of the resulting vector v: __________
Do NOT try at home: Child towing a RipStik with a bicycle The bicycle provides a force of 100 Newtons at an angle of 20° to the horizontal. The RipStik generates a drag of 50 Newtons at an angle of 180° to the horizontal. What is the direction angle and magnitude of the net force on the RipStik? Add the two vectors to determine the resulting direction angle and magnitude of the net force.
magnitude of net force: ____________
direction angle in degrees of net force: ____________