ABCDEFGHIJKLMNOPQRSTUVWXYZ abcdefghijklmnopqrstuvwxyz 0123456789-= ~!@#$%^&*()_+ ;',./:"<>?[]\{}|.
The strength of a random password as measured by the information entropy. The formula for a random password's information entropy, H, is given by the function:
H = (Length of the password ) log2(Number of characters available)
H = L log2N
where H is reported in bits of entropy. Note that the log is the base 2 logarithm.
- H = _____________ bits. For a random password with a length of eight (L = 8) which uses lowercase, uppercase, numbers, and symbols (number of possible characters N to choose from is 95), calculate the bits of entropy.
- L = _____________ Some IT pundits recommend that random passwords have 72 bits of entropy. Use the function above with an N equal to 95 characters. Calculate the length L necessary to obtain H = 72 bits of entropy.
- L = _____________ Most computer users only use lowercase and uppercase letters, which is only 52 possible characters for their password. With N equal to 52 characters, Calculate the length L necessary to obtain H = 72 bits of entropy.
- _____________ What is the length in characters of the passwords you usually use? [open answer].
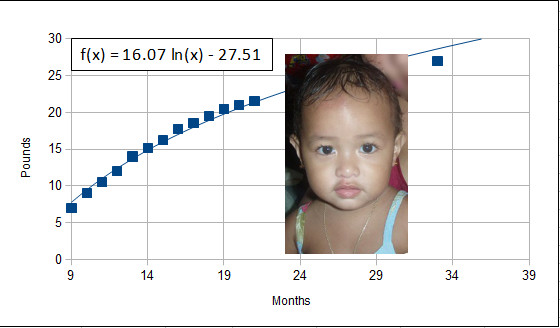 The chart depicts a baby weight function for a baby that grew at
The chart depicts a baby weight function for a baby that grew atf(x) = 16.07 ln(x) − 27.51 where x is the months since conception and f(x) is the weight in pounds. Birth is at x = 9 months. The y-axis is the weight of the baby in pounds.
- ____________ Calculate the birth weight of the baby by evaluating the growth function at x = 9 months.
- ____________ Calculate the weight of the baby at x = 21 months (one year post birth).
Either make the calculation or solve for x as appropriate. Round answers to two decimal places.
| Distance | Sound volume |
|---|---|
| 10 | 100 |
| 20 | 60 |
| 30 | 40 |
| 50 | 20 |
| 80 | 0 |
Use a spreadsheet to plot the logarithmic sound attenuation model. Add a logarithmic trend line and equation.
- Write the logarithmic function:
- _________ Use the logarithmic function to calculate the volume for a distance of 65.
- _________ Use the logarithmic function to calculate the distance for a volume of 80.
- ( ________ , _________ )
- ( ________ , _________ )
- ( ________ , _________ )
- ( ________ , _________ )