| Day | Density (kg/m³) |
|---|---|
| 1 | 156 |
| 2 | 160 |
| 3 | 161 |
| 4 | 162.5 |
| 5 | 163 |
| 6 | 163.5 |
| 7 | 164 |
| 8 | 165.5 |
| 9 | 166 |
| 10 | 166.5 |
| 11 | 166.7 |
| 12 | 167 |
| 13 | 167.5 |
| 14 | 169 |
| 15 | 169.5 |
| 16 | 170 |
| 17 | 171 |
- Graph the data, add a LOGARITHMIC trend line and equation to the graph, and then write the logarithmic equation:
- ____________ Based on the logarithmic equation in part a, calculate the density for day 36.
- ____________ Based on the logarithmic equation in part a, calculate the day when the density would be predicted to be 175 kg/m³
- Solve the equation in part a for x, writing out the resulting inverse equation below:
- ____________ 140
- ____________ log1414
- ____________ log 10000
- ____________ ex = 8103.09
- ____________ ln x = 2.7726
- ____________ log5x = 2
- ____________ 6 ln(6x) = 32.2517
- ____________
- ____________ ln(2) + ln (32) = ln(x)
- ____________ 2 log(3) − log(x + 144)= −2 log(5)
- ____________
= _________° = _________° = _________°
- __________ What marker shape is f(x) = ex?
- __________ What marker shape is f(x) = e−x?
- __________ What marker shape is function f(x) = ?
- ________________ What is the name of the type of function seen in letter c?
- ________________ On the 12th of June I introduced the function seen in letter c as being characteristic of the time versus velocity for what sport?
- __________________ Calculate: 100 sin(72°)
- __________________ Calculate: 100 cos(72°)
- __________________ Calculate: 100 tan(72°)
- __________________ Calculate: 100 sin(36°)
- __________________ Calculate: 100 cos(36°)
- __________________ Calculate: 100 cos(36°)
- __________________ Calculate: 100 sin(18°)
- __________________ Calculate: 100 cos(18°)
- __________________ Calculate: 100 tan(18°)
- __________________ Calculate: 100 sin(0°)
- __________________ Calculate: 100 cos(0°)
- __________________ Calculate: 100 tan(0°)
- __________________ Calculate: 100 tan(90°)
- ( ________ , _________ )
- ( ________ , _________ )
- ( ________ , _________ )
- ( ________ , _________ )
- ( ________ , _________ )
Wave equation in terms of period τ and time t:
Period τ and frequency f relationship:
- a = _______________ Write the amplitude a of the equation.
- λ = _______________ Write the wavelength λ of the equation.
- a = _______________ Write the amplitude a of the equation.
- τ = _______________ Write the period τ of the equation.
- f = _______________ Calculate the frequency f of the equation.
- ________ How many waves are shown in the diagram?
- λ = _______________ Write the wavelength λ
- a = _______________ Write the amplitude a.
- τ = _______________ Write the period τ.
- f = _______________ Calculate the frequency f.
- y = ______ sin( _________ x). Write out the equation of the wave in terms of the wavelength λ and distance x.
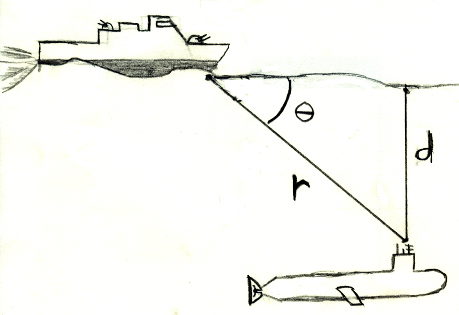 Depth charges are explosives that detonate at a specific depth d under the surface of the water. A destroyer armed with depth charges is using a sonar to determine the angle θ and the distance r to a submarine.
Depth charges are explosives that detonate at a specific depth d under the surface of the water. A destroyer armed with depth charges is using a sonar to determine the angle θ and the distance r to a submarine.
- Write an equation for the angle θ in terms of r and d:
- d = _________ If the angle θ = 40° and the range r is 156 meters, what is the value of the depth d?
For a MicroGames javelin thrown at a velocity v = 8 m/s at θ = 40°
- vx = ______________ Calculate the horizontal velocity vx
- vy = ______________ Calculate the vertical velocity vy
- d = _____________Calculate the distance d the javelin will travel.
- magnitude = __________ Calculate the magnitude.
- θ = __________ Calculate the direction angle in degrees.
= ________ i + ________ j
- F ⋅ d ___________ Calculate the energy (work) done to move the object 10 meters using the dot product.
- F ⨯ d ___________ Calculate the torque on the object if the lever arm distance is 0.3 meters using the cross product.
Write the matrix A + B | Write the matrix A − B | Write the matrix 2A