pse3 064 test 02 midterm ☈ Name:

  1. A student measures a 45 gram bar of soap with a length of 9.0 cm, a width of 3.0 cm, and a height of 2.0 cm.
    1. __________ _____ What is the volume of the soap?
    2. __________ _____ What is the density of the soap?
    3. ______________ Will the soap float or sink?
    4. ______________ What brand of soap is this?
  2. For the following RipStik velocity data and chart:
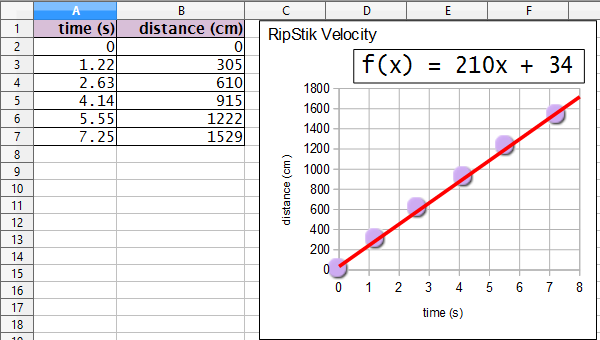
    RipStik velocity, time versus distance
    1. __________ _____ Determine the velocity ѵ of the RipStik.
    2. __________ _____ If the RipStik continued at that velocity for 60 seconds, how many centimeters would the RipStik travel?
    3. __________ _____ If the RipStik continued at that velocity for 1819 centimeters, how many seconds would the RipsStik travel?
  3. Grid 12 x 10 on the thirties background rectangle major grid lines axes Line data points as circles text layers RipStick Deceleration Run time (seconds) distance (centimeters) y-axis labels 0 100 200 300 400 500 600 700 800 900 1000 x-axis labels 0 1 2 3 4 5 6 7 8 9 10 11 12 Image block RipStik Rider The graph shows RipStik deceleration data. A RipStik was ridden 900 centimeters up a gentle slope, then the RipStik was ridden back down the same slope. The time from the start at the bottom of the slope to the return to the bottom of the slope was 12 seconds.
    1. __________ _____ Determine the velocity at exactly 6 seconds.
    2. __________ _____ Calculate the velocity between 8 and 10 seconds.
    3. __________ _____ Calculate the velocity between 10 and 12 seconds.
    4. __________ _____ Calculate the acceleration between 10 and 12 seconds.
  4. A superball falls for 700 centimeters from the height of the new windows in the FSM-China Friendship Sports Center.
    1. __________ _____ How long does the superball fall in seconds?
    2. __________ _____ What is the speed of the superball?
  5. A child on a RipStik starts from a speed of zero at a vertical height of 0.30 meters above the bottom of a slope. The mass of the child and the RipStik is 30 kg. The acceleration of gravity g is 9.79 m/s².
    1. _________ __________ Calculate the Gravitational Potential Energy of the child and RipStik at the top of the slope.
    2. _________ __________ Use the relationship Kinetic Energy = Gravitational Potential Energy to calculate the speed of the child and the RipStik at the bottom of the slope.
    3. _________ __________ Use the velocity to calculate the momentum of the child and RipStik at the bottom of the slope.
  6. Mathematical models Mathematical models on the half shell background rectangle major grid lines axes x-axis and y-axis a square root path a quadratic path a rational function with asymptote path data points as circles linear regression line data points as rectangles data points as diamonds text layers Mathematical relationships x-axis labels A B C D
    1. _____ Identify by the letter which of the mathematical relationships on the graph represents the time versus distance relationship for a RipStik moving at a constant linear velocity with no acceleration (as in the homework 021 in the second week).
    2. _____ Identify by the letter which of the mathematical relationships on the graph represents the time versus distance relationship for a ball falling under the constant acceleration of gravity g (as in laboratory three).
    3. _____ Identify by the letter which of the mathematical relationships on the graph represents the height versus velocity relationship for a marble rolling from a height h down a banana leaf and onto a flat table (homework 041).
    4. _____ Identify by the letter which of the mathematical relationships on the graph represents the length versus mass for a cantilever (as last Friday in class, homework 054).
  7. A student rolled a single marble three times into a line of five marbles. The first roll was a slow roll, the second was a fast roll, and the third roll was faster.
    Marbles on ruler track
    The student gathered the following data:

    Slow marble in: distance = 24 cm, time = 1.2 seconds.
    Slow marble out: distance = 24 cm, time = 1.6 seconds.
    Fast marble in: distance = 24 cm, time = 0.75 seconds.
    Fast marble out: distance = 24 cm, time = 1.0 seconds.
    Faster marble in: distance = 24 cm, time = 0.6 seconds.
    Faster marble out: distance = 24 cm, time = 0.8 seconds.

    1. Use the data above to calculate the velocity in and the velocity out. Record the velocities in the table below.
      Graphical analysis SVG with embedded table

      Velocity

      Marblevelocity
      in (cm/s)      		velocity out
      (cm/s)
      At rest00
      Slow
      Fast
      Faster
      background rectangle major grid lines axes text layers Velocity chart velocity in (cm/s) velocity out (cm/s) y-axis labels 0 4 8 12 16 20 24 28 32 36 40 y 0 4 8 12 16 20 24 28 32 36 40 44
    2. _________ __________ Calculate the slope of the line.
    3. _________ __________ Determine the y-intercept of the line.
    4. ___________ Was velocity gained or lost?
    5. _________ __________ For a velocity in of 60 cm/s, what is the predicted velocity out based on the data above?
    6. _________ __________ For a velocity out of 42 cm/s, what is the predicted velocity in based on the data above?
  8. Double balloon Front view Top view If air is blown between the two balloons, will the balloons move towards each other or away from each other?


    What is the name of the law that causes the balloons to move as they do?

  9. Use the data to answer the following questions on pulleys.
    force (gmf)load (gmf)
    2066
    80264
    140462
    180594
    1. ____________ What is the actual mechanical advantage for the pulley system?
    2. ____________ The pulley system had four load lines. What is the ideal mechanical advantage?
    3. ____________ Use the preceding two questions to calculate the efficiency of the pulley system.
  10. Write out Newton's first law.
  11. Give a mathematical statement of Newton's second law.
  12. Write out Newton's third law.
  13. Temperatures in Celsius:

slope= ( y2 − y1 ) ( x2 − x1 )
ѵ= Δd Δt
distance d = velocity ѵ × time t
a = Δѵ Δt = ( v2 − v1 ) ( t2 − t1 )
ѵ = at
ѵ = gt
d = ½at²
d = ½gt²
where g is the acceleration of gravity, g = 979 cm/s²

Gravitational Potential Energy GPE = mgh
Kinetic Energy KE = ½mѵ²
KE=mѵ2 2
momentum = mass m × velocity ѵ
Force F = mass m × acceleration a

Actual Mechanical Advantage = Load lifted ÷ Force used to lift
efficiency= Actual Mechanical Advantage Ideal Mechanical Advantage