- __________ _____ Calculate the density ρ of Dial Basic soap.
- ______________ Based on the density, will Dial Basic soap float or sink?
- __________ _____ Using the density above, calculate the mass of a bar of Dial Basic soap that has a volume of 100 cm³.
- __________ _____ Using the density above, calculate the volume of a bar of Dial Basic soap that has a mass of 250 grams.
- __________ _____ Calculate the density ρ of Ivory soap.
- ______________ Based on the density, will Ivory soap float or sink?
- __________ _____ Calculate the density ρ of Neutrana soap.
- ______________ Critical thinking: Based on the density, will Neutrana soap float or sink?
- __________ _____ Determine the velocity ѵ of the RipStik.
- __________ _____ If the RipStik continued at that velocity for 30 seconds, how many centimeters would the RipStik travel?
- __________ _____ If the RipStik continued at that velocity for 7500 centimeters, how many seconds would the RipStik travel?
- Plot the data using circles, squares, and diamonds for A, B, and C respectively.
- __________ __________ Calculate the velocity (speed) of RipStik run A.
- __________ __________ Calculate the velocity (speed) of RipStik run B.
- __________ __________ Calculate the velocity (speed) of RipStik run C.
- __________ __________ How far will RipStik A travel in 36 seconds?
- __________ __________ How long in seconds for RipStik A to travel 5100 centimeters?
- __________ __________ What was the speed of the RipStik at time t = 0 seconds?
- __________ __________ Use the data provided and the slope formula to calculate the velocity (speed) of the RipStik from 9 to 10 seconds.
- __________ __________ Using the velocity at t = 0 seconds from a) above and the velocity of the RipStik from 9 to 10 second from b) above, calculate the acceleration of the RipStik.
- __________ __________ Calculate the Gravitational Potential Energy of the marble before the marble is released using GPE = mgh
- __________ __________ Calculate the velocity that the same marble should have at the bottom of the ramp using the equation KE = ½mѵ² if there is no friction.
- Why are the marbles in generally equal to the marbles out?
- For balls swinging from a pendulum the number in is equal to the number out. For marbles this is generally but not exactly true. What is different about the marbles that complicates the "number in" being equal to "the number out"?
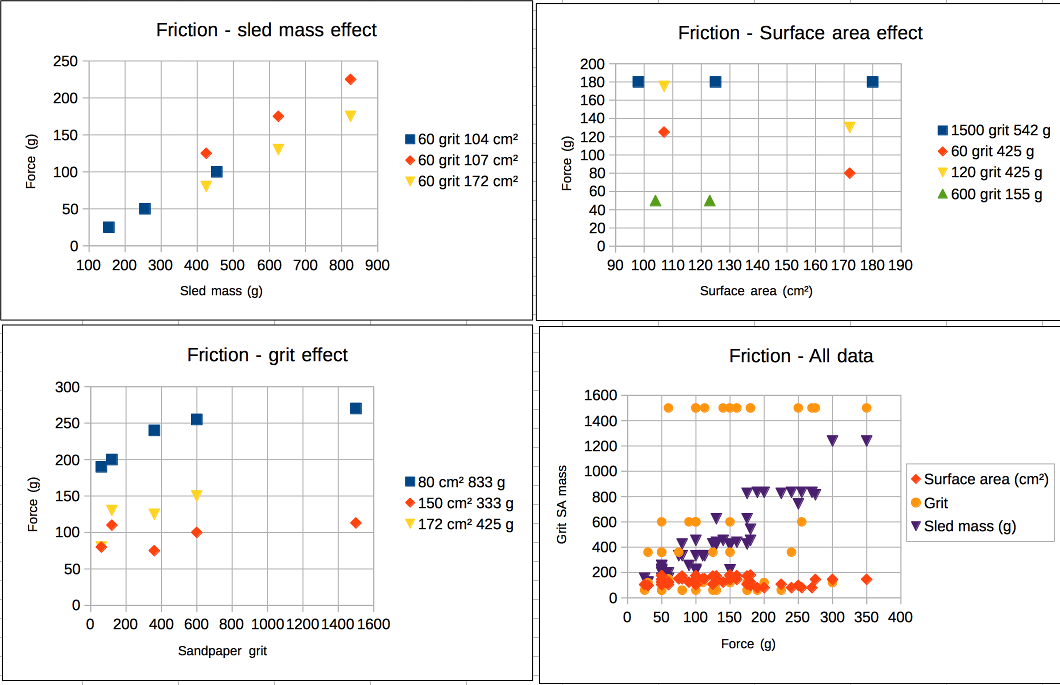
- __________ Calculate a reasonable estimate of the slope of the best fit trend line for the sled mass (g) versus the Force (g).
- For part a) above, what are the units?
- _________℃ What is the temperature of a mix of melting ice and water?
- _________℃ What is the typical daily in Pohnpei?
- _________℃ What is the temperature of the healthy living human body?
- _________℃ What is the temperature of a boiling water?
- _________ _____ The drain grating is at E 158° 09.663'. Binky was at E 158° 09.319'. Calculate the difference in arc minutes between the drain grating and Binky.
- Use the difference in arc minutes from part a) and the published value of 1842 meters per arc minute of longitude here on Pohnpei to calculate the distance in meters from the grating to Binky.
- ___________ ____________ Determine the slope of the line.
- ___________ ____________ Use the slope to calculate the number of meters for 10 arcminutes.
- ___________ ____________ Use the slope to calculate the number of meters for 0.001 arcminutes.
- ___________ ____________ Use the slope to calculate the number of arcminutes for 5000 meters.
Volume V = length l × width w × height h
mass m = density ρ × Volume V
distance d = velocity ѵ × time t
velocity ѵ = acceleration a × time t
ѵ = gt
d = ½at²
d = ½gt²
where g is the acceleration of gravity
g = 980 cm/s²
Gravitational Potential Energy GPE = mgh where the acceleration of gravity g = 980 cm/s²
Kinetic Energy KE = ½mѵ²
momentum p = mass m × velocity ѵ