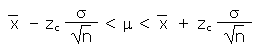
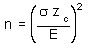
For the following data:
| HS | TOEFL Student Count n | TOEFL Sample Mean | TOEFL stdev sx |
|---|---|---|---|
| CCA | 12 | 529 | 64 |
For the above data a 95% confidence interval has an error E for the TOEFL mean of 36.21 Suppose I want to reduce that Error E to 20 for a 99% confidence interval, how many students would need to be in the sample? Please note that both the desired Error E and the confidence level c are changed.
| Statistic | Equation |
|---|---|
| Calculate a confidence interval for a mean m for large n (n>30) using the population deviation s | 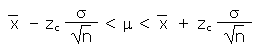 |
| Calculate a confidence interval for a mean m for large n (n>30) using the sample deviation s | |
| Confidence interval for m and s for n < 30. | |
| Sample size calculations | 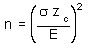 |
| Level of Confidence c | Critical value zc |
|---|---|
| .80 | 1.28 |
| .85 | 1.44 |
| .90 | 1.645 |
| .95 | 1.96 |
| .99 | 2.58 |