Images	Horsepower	Price/1000s
	275	155
	300	175
	350	230
	365	240
	400	280
	525	280
	650	400
	760	450
	1050	600
	1775	1000

For this midterm all questions use the data given in the table containing information about Terex off highway dump trucks. The Terex line of off highway dump trucks runs from a 275 horsepower articulated dump truck for $155,000 to a 1775 horsepower rigid frame truck $1,000,000. The y-data given in the table is in 1000's of dollars.

Perform a linear regression for the accompanying Terex Off Highway Trucks using horsepower versus price data.

1. Calculate the slope of the best fit line for the horsepower and price data
   
   
2. Calculate the y-intercept for the data
   
   
3. Is the correlation positive, negative, or neutral?
   
   
4. Determine the correlation coefficient
   
   
5. Is the correlation none, low, moderate, high, or perfect?
   
   
6. Determine the coefficient of determination
   
   
7. What percent in the variation in horsepower explains the variation in price?
   
   
8. Based on the equation of the best fit line, what would be the predicted price in dollars for a 900 horsepower truck?
   
   
9. Based on the equation of the best fit line, what would be the projected horsepower of a $300,000 dollar truck? Remember that your y-axis is in 1000's of dollars.
   
   Use the horsepower data to perform the following calculations:
   
   
10. Find the sample size n:
11. Find the minimum horsepower:
12. Find the maximum horsepower:
13. Find the range horsepower:
14. Find the median horsepower:
    
    
15. Find the mode horsepower:
    
    
16. Find the sample mean horsepower:
    
    
17. Find the sample standard deviation horsepower:
    
    
18. Find the sample coefficient of variation CV:
    
    
19. If this data is to be divided into four bins what is the width of a single bin?
    
    
20. Determine the frequency and calculate the relative frequency using four bins. Record your results in the table provided.

    Bins (x)	Frequency (f)	P(x)
    _______	_______	_______
    _______	_______	_______
    _______	_______	_______
    _______	_______	_______
    Sum:	_______________	_______________

21. Sketch a relative frequency histogram of the data here below or on the back, labeling your horizontal axis and vertical axis as appropriate.
    
    
22. What is the shape of the distribution?
    
    
23. Determine P(650 < horsepower <= 1025)
    
    
24. Determine P(x > 1025)

Statistic or Parameter	Symbol	Equations	Excel
Square root			=SQRT(number)
Sample mean		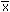Sx/n	=AVERAGE(data)
Sample standard deviation	sx		=STDEV(data)
Sample Coefficient of Variation	CV	100(sx/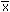)	=100*STDEV(data)/AVERAGE(data)
Slope	b		=SLOPE(y data, x data)
Intercept	a		=INTERCEPT(y data, x data)
Correlation	r		=CORREL(y data, x data)
Coefficient of Determination	r²		=(CORREL(y data, x data))^2

Statistics home Lee Ling home COM-FSM home page