| ____ 1. Grades: A, B, C, D, F | A. Nominal | |
| ____ 2. Favorite soy sauce: Angostura, Kikkoman, Sanbushi, Yamasa | B. Ordinal | |
| ____ 3. Year: 1981, 1987, 1999, 2002 | C. Interval | |
| ____ 4. Soy sauce bottle volumes: 500ml, 1000ml, 1800ml | D. Ratio |
The table is of retail prices for 1000 ml soy sauce on Pohnpei on 04 September 2002
| Store | Brand | Price |
|---|---|---|
| Nakasone | Sanbushi | 2.60 |
| Wall Mart | Kikkoman | 3.27 |
| Yoshie | Kikkoman | 3.45 |
| Palm Terrace | Kikkoman | 3.69 |
| Ambros | Kikkoman | 3.85 |
| Best Buy | Kikkoman | 3.89 |
| Josaiah | Kikkoman | 3.90 |
| Ace Commercial | Yamasa | 3.95 |
| Nakasone | Kikkoman | 3.97 |
| 4TY | Yamasa | 4.25 |
| Panuelo | Yamasa | 4.75 |
| En's Seven Star | Yamasa | 4.95 |
| Bins | Frequency | Relative Frequency |
|---|---|---|
| _______ | _______ | _______ |
| _______ | _______ | _______ |
| _______ | _______ | _______ |
| _______ | _______ | _______ |
| _______ | _______ | _______ |
| Sum: | _______ | _______ |
Sunday evening I ran 14 laps of the track with a mean lap time of 2.59 minutes and standard deviation of 8.00 seconds. Construct a 95% confidence interval using a student's t-distribution for my population mean lap time.
| Confidence interval statistics | |||
|---|---|---|---|
| Find a tc value from a confidence level c and sample size n | tc | =TINV(1-c,n-1) | |
| Calculate an error tolerance E of a mean for any n ≥ 5 using sx. | E | =tc*sx/SQRT(n) | |
| Calculate a confidence interval for a population mean µ from a sample mean x and an error tolerance E | x-E≤ µ ≤x+E | ||
| Hypothesis Testing | |||
| Degrees of freedom | df | = n-1 | =COUNT(data)-1 |
| Calculate a t-statistic (t) | t | 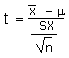 |
(x - µ)/(sx/sqrt(n)) |
| Calculate t-critical for a two-tailed test | tc | =TINV(α,df) | |
| Calculate a p-value from a t-statistic t | p | = TDIST(ABS(t),df,#tails) | |