MS 150 Stat Q09 Fall 2005 p-value • Name: _______________

The human heart has a mean resting heart rate (RHR)of 72 beats per minute (bpm). The table gives the heart rates for students in ESS 101j Joggling class. Calculate the sample mean and sample standard deviation for the data. Perform a hypothesis test that the class RHR is different from the expected population mean resting heart rate µ of 72 bpm at a significance of 5%

1. _________ Find the sample size n for the resting heart rate data.
2. _________ Find the sample mean x resting heart rate.
3. _________ Find the sample standard deviation sx of the resting heart rate.
4. Write out the null hypothesis: H₀:
5. Write out the alternate hypothesis: H₁:
6. _________ What is alpha α?
7. _________ How many degrees of freedom are there?
8. _________ Determine t_c
9. _________ Find the t-statistic t.
10. Do we:
    1. ___ Reject the null hypotheis? OR
    2. ___ Fail to reject the null hypothesis?
       
       
11. ___________________________ Is the class resting heart rate significantly different from the expected population mean of 72?
12. _________ What is the p-value for this hypothesis test?
13. _________ What is the largest possible confidence interval for which this difference is significant?
14. _________ Look at the p-value. Would the sample be statistically significantly different at an significance of 10%?

Statistic or Parameter	Symbol	Equations	Excel
Hypothesis Testing
Degrees of freedom	df	= n-1	=COUNT(data)-1
Calculate a t-statistic (t)	t		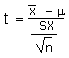(x - µ)/(sx/sqrt(n))
Calculate t-critical for a two-tailed test	tc		=TINV(α,df)
Calculate a p-value from a t-statistic t	p		= TDIST(ABS(t),df,#tails)