Test 02 9-10 Confidence interval hypothesis test answer sheet

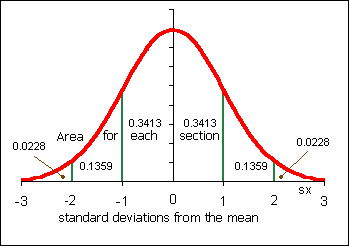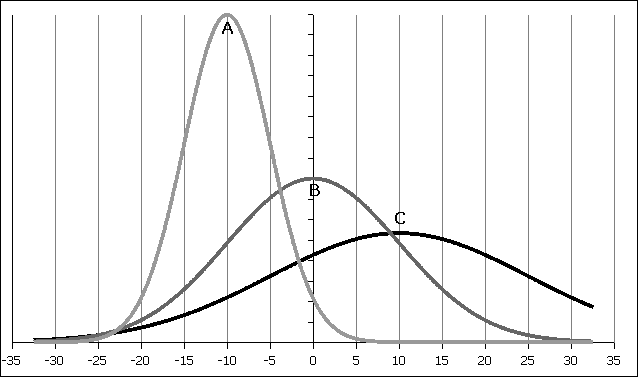
1. For the following curves A, B, and C determine the mean µ and the standard deviation σ:

2. Using global positioning satellite systems, the length of lane four at the Pohnpei state track facility was measured nine times. Use the data in the table to determine the sample mean x and the sample standard deviation sx. Use this data to calculate a 95% confidence interval for the population mean lane four length.

1. confidence level: c = 0.95
2. degrees of freedom: = 8
3. t-critical: t_c = 2.3060
4. Error tolerance E: = 3.0208
5. Calculate the confidence interval for the population mean lane four length:
   
   P( 434 ≤ µ ≤ 440 ) = 0.95
6. No. The international standard for the length of lane four is 424 meters. With a 95% level of certainty, does the confidence interval for lane four at the Pohnpei state track include this value?
7. No. Does lane four of the Pohnpei state track conform to international standards?
8. Too long. Will times run in lap four likely to too short or too long versus a track with lane four at the international standard length?

Confidence interval statistics
Find a tc value from a confidence level c and sample size n	tc		=TINV(1-c,n-1)
Calculate an error tolerance E of a mean for any n ≥ 5 using sx.	E		=tc*sx/SQRT(n)
Calculate a confidence interval for a population mean µ from a sample mean x and an error tolerance E		x-E≤ µ ≤x+E