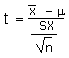
A sample size n = 43 students had their body fat measured in January and again in May. There was a sample mean xdifference = 0.44 change in the paired differences with a standard deviation of sx = 1.40
Run a hypothesis test that this data could not include a population mean µdifference = 0. For this test the hypothesis of no change, the null hypothesis, is:
H0: µdifference = 0.
The alternate hypothesis is that a change has occurred, that a the data taken could not include the possibility of a change of zero, is:
H1: µdifference ≠ 0
Run the hypothesis test at an alpha of α = 0.05
A sample size n = 38 students took the Duke Kahanamoku pre-test and post-test. There was a sample mean xdifference = 0.89 change in the paired differences with a standard deviation of sx = 1.16
Run a hypothesis test that this data could not include a population mean µdifference = 0. For this test the hypothesis of no change, the null hypothesis, is:
H0: µdifference = 0.
The alternate hypothesis is that a change has occurred, that a the data taken could not include the possibility of a change of zero, is:
H1: µdifference ≠ 0
Run the hypothesis test at an alpha of α = 0.05
| Statistic or Parameter | Symbol | Equations | Excel |
|---|---|---|---|
| Hypothesis Testing | |||
| Degrees of freedom | df | = n-1 | =COUNT(data)-1 |
| Calculate t-critical for a two-tailed test | tc | =TINV(α,df) | |
| Calculate a t-statistic (t) | t | 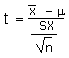 |
(x - µ)/(sx/sqrt(n)) |
| Calculate a p-value from a t-statistic t | p | = TDIST(ABS(t),df,#tails) | |
| Calculate a maximum possible level of confidence c from a p-value (two-tailed) | max c = 1-p | ||