MS 150 Statistics spring 2006 test one • Name:

For each type of data shown write the appropriate measure of the middle and, if any, the appropriate measure of the spread of the data. For each data type, determine the appropriate value for the middle. Think of this problem this way: imagine a friend has brought the following three sets of data to you and asks you to determine the middle and spread.

Data set one: Favorite colors: blue, red, orange, yellow, green, cyan, blue, indigo, purple, violet, magenta, blue
Data set two: Sakau market ratings (cups until sakaula):
Pwopwida: | Song ie mahs: | Stroke:
6-11: | No choice:
Data set three: Prices of ramen in cents: 25, 35, 55, 100

Data set	Level of measurement	Appropriate function to measure middle	Value of the middle measure	Appropriate function to measure spread	Value of the spread measure
1.	nominal	mode	blue	(none)	(n/a)
2.	ordinal	median		range
3.	ratio	mean	53.75	stdev	33.26

For the favorite number data seen at the left:

1. 12 Find the sample size n.
2. 1 Find the minimum.
3. 17 Find the maximum.
4. 16 Find the range.
5. 5 Find the median.
6. 5 Find the mode.
7. 6.25 Find the sample mean x.
8. 4.63 Find the sample standard deviation sx.
9. 0.74 Find the sample coefficient of variation CV.
10. 4 If this data is to be divided into four bins, what is the width of a single bin?
11. Determine the frequency and calculate the relative frequency using four bins (classes, intervals). Record your results in the table provided.

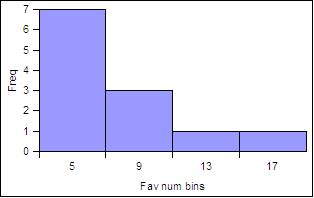
    Bins	Frequency	Relative Frequency
    5	7	0.58
    9	3	0.25
    13	1	0.08
    17	1	0.08
    Sums:	12;	1.00

12. Sketch a frequency histogram of the data, labeling your horizontal axis and vertical axis as appropriate. Use the back of this sheet if necessary.
13. skewed What is the shape of the histogram?