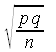
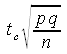
| Dollars per year |
|---|
| 46000 |
| 71000 |
| 18000 |
| 89000 |
| 49000 |
| 81000 |
The table provides the amount of money raised per year over a six year period for the endowment fund. The endowment fund is intended to help fund the college after Compact II expires in 2023. Construct a 95% confidence interval for the population mean μ money raised per year.
A sample size n of 1541 8th grade students in the FSM took the National Standards Test in mathematics administered in 2006. 189 students of the 1541 achieved 80% correct or better - a level that the FSM refers to as mastery of the material. This represents a sample success proportion p in percentage of 12.26% of the students. Find the 95% confidence interval for the population proportion P.
Formulas are written for OpenOffice.org Calc. Replace semi-colons with commas for Excel.
| Confidence interval statistics | |||
|---|---|---|---|
| Statistic or Parameter | Symbol | Equations | OpenOffice |
| Find the limit for a confidence interval for n ≥ 30 using a normal distribution with p as the area to the left of the limit | =NORMINV(p;μ;σ/SQRT(n)) | ||
| Degrees of freedom | df | = n − 1 | =COUNT(data)-1 |
| Find a t-critical tc value from a confidence level c and sample size n | tc | =TINV(1-c;n-1) | |
| Standard error of the mean | σx |
|
=sx/SQRT(n) |
| Calculate the margin of error E for a mean for any n ≥ 5 using sx. | E | =tc*sx/SQRT(n) | |
| Calculate a confidence interval for a population mean μ from the sample mean x and margin of error E for the mean. | x − E ≤ μ ≤ x + E | ||
| Number of successes or desired results in a sample | r | ||
| Proportion of successes or desired result in a sample | p | r ÷ n | =r/n |
| Proportion of non-successes, not the desired, or alternate result in a sample | q | 1 − p | =1-p |
| Standard error of a proportion p | σx |
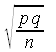
|
=SQRT(p*q/n) |
| Margin of error E for a proportion p | E |
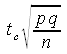
|
=TINV(1-c;n-1)*SQRT(p*q/n) |
| Calculate a confidence interval for a population proportion P from the sample proportion p and the margin of error E for the mean. | p − E ≤ P ≤ p + E | ||