| Cups |
|---|
| 3 |
| 3 |
| 3.5 |
| 3.5 |
| 2 |
| 3 |
| 4 |
| 1 |
| 8 |
| 3 |
| 9 |
| 3 |
| 7 |
| 6 |
| 7 |
| 10 |
| 5 |
| 4 |
| 2 |
| 2 |
| 1 |
| 1.5 |
| 7 |
| 2 |
| 3.5 |
| 1.5 |
| 1 |
| 8 |
| 3 |
| 3 |
The final examination this term takes its data from a local business example. Although the business is unique, the analysis would apply to any small business operating in a highly competitive environment. The data on the right records the number of cups purchased per person at Song Mahs sakau en Pohnpei market for 30 customers on one evening. The data is also available in a data sheet to save you retyping the data.
For the number of cups data given in the table:
| Bins | Frequency | RF p(x) |
|---|---|---|
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| Sums: | _________ | _________ |
Data on the number of cups purchased per person for 193 customers was gathered from Nan kahp, Pwopwihda, Rush Hour, and Song Mahs markets.
| Bins x (cups) | Freq f | RF or P(x) | x*P(x) |
|---|---|---|---|
| 1 | 39 | 0.202 | 0.20 |
| 2 | 46 | 0.238 | 0.48 |
| 3 | 47 | 0.244 | 0.73 |
| 4 | 31 | 0.161 | 0.64 |
| 5 | 14 | 0.073 | 0.36 |
| 6 | 16 | 0.083 | 0.50 |
| Sums: | 193 | 1.000 | 2.91 |
A sample size n of twenty-seven customers at Nan kahp market purchased a sample mean x 3.19 cups with a sample standard deviation sx of 2.06 cups. Construct a 95% confidence interval for the population mean µ number of cups for Nan kahp based on the data provided. Note that n is less than 30.
A sample size n = 27 customers at Nan kahp sakau market purchased a sample mean x = 3.19 cups with a sample standard deviation sx = 2.06 cups. A study across multiple nights and a number of different markets on Pohnpei established a population mean µ = 3.65 cups purchased per customer. If the Nan kahp data is statistically significantly different than the population mean, then Nan kahp sakau could be theorized to be stronger than average (3.19 is fewer than 3.65, fewer implies stronger). Run a two-tailed hypothesis test with an alpha of α = 0.05 to test whether the Nan kahp sample mean is statistically significantly different from the known population mean of 3.65 cups.
| Market | distance /kilometers | mean cups per customer |
|---|---|---|
| Rush Hour | 3.0 | 5.18 |
| Song Mahs | 13.5 | 3.93 |
| Nan kahp | 14.0 | 3.19 |
| Pwopwida | 15.5 | 2.62 |
The data in this section examines whether there is a trend in the mean number of cups of sakau purchased per customer with increasing distance in kilometers from Spanish Wall in Kolonia. Zero kilometers is at Spanish Wall.
The data on this final is based on actual data from real markets here on Pohnpei. The author is deeply indebted to the markets for sharing their proprietary information.
The average number of cups per customer refers to individual named customers. The original data is contained in a separate spreadsheet, minus the customer names.
The average number of cups consumed is not necessarily an indication of the strength of the sakau. Some markets cater to commuters who tend to drink a cup or two on their way home and then head on home. Other markets are destination markets at which customers linger late into the evening engaged in the fine art of conversation.
| Basic Statistics | |||
|---|---|---|---|
| Statistic or Parameter | Symbol | Equations | OpenOffice |
| Square root | =SQRT(number) | ||
| Sample standard deviation | sx or s | =STDEV(data) | |
| Sample Coefficient of Variation | CV | sx/x | =STDEV(data)/AVERAGE(data) |
| Confidence interval statistics | |||
|---|---|---|---|
| Statistic or Parameter | Symbol | Equations | OpenOffice |
| Degrees of freedom | df | = n-1 | =COUNT(data)-1 |
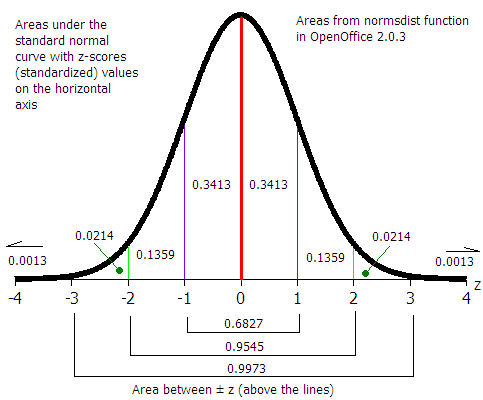
| Find a zc value from a confidence level c | zc | =ABS(NORMSINV((1-c)/2)) | |
| Find a tc value from a confidence level c | tc | =TINV(1-c;df) | |
| Calculate a margin of error for the mean E for n < 30 using sx. Should also be used for n ≥ 30. | E | =tc*sx/SQRT(n) | |
| Calculate a confidence interval for a population mean µ from a sample mean x and an error tolerance E | x - E ≤ µ ≤ x + E | ||
| Hypothesis Testing | |||
| Calculate t-critical for a two-tailed test | tc | =TINV(α;df) | |
| Calculate a t-statistic | t | 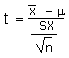 |
=(x - µ)/(sx/SQRT(n)) |
| Calculate a two-tailed p-value from a t-statistic | p | = TDIST(ABS(t);df;2) | |
| Linear Regression Statistics | |||
|---|---|---|---|
| Statistic or Parameter | Symbol | Equations | OpenOffice |
| Slope | b | =SLOPE(y data; x data) | |
| Intercept | a | =INTERCEPT(y data; x data) | |
| Correlation | r | =CORREL(y data; x data) | |
| Coefficient of Determination | r2 | =(CORREL(y data; x data))^2 | |